Bend Loss: A form of increased Attenuation in a Fiber that results from bending a fiber around a restrictive curvature (a macro bend) or from minute distortions in the fiber (micro bends). 2. A form of increased attenuation caused by allowing high order Modes to radiate from the walls of a fiber optic cable. There are 2 common types of bend losses. The first type results when the fiber optic Cable is curved through a restrictive radius or curvature. The second type is generally referred to as micro bends. It is caused by small distortions of the Fiber Optic Cable imposed by externally induced perturbations as, for Example, slip shod cabling techniques.

Types of Bends:

Conduit installations are normally referred to as runs of conduit. A run of conduit is the conduit, fittings, straps, conductors, and bends needed from one opening to the next (for example, from the panel board to the first outlet box or from the first outlet box to the second outlet box). In a run of conduit, there cannot be more than the equivalent of four 90° bends, for a total of 360°. The purpose of allowing only so many bends in a run of conduit is to help in pulling conductors into the conduit. Experience has taught that if more than 360° of bends are used, it is very difficult to pull conductors through the bends Figure 1

Figure: 1 360° bendConduit bodies are available in the following configurations: elbow back (LB), elbow right (LR), and elbow left (LL) and a T. The configuration of each is determined based on the location of the removable cover Figure 2

Figure: 2 Conduit bodies

By using a conduit body in a run, you provide an opening for pulling the conductors without having to mount a box. At the same time, you can make a turnaround or go over an obstacle and maintain a neat conduit installation. The turn or 90° turn made by the conduit body does not count as one of the four allowable bends in a run. As a matter of fact the conduit body is identified as an outlet box. One of the most common bends you will make in the field is the right-angle bend, more commonly called a 90° bend or just a 90. It can be used for going around an inside corner, into the top or bottom of a box from a horizontal run, or over an object. Anyone can make a 90° bend in a stick of conduit and then cut it off to make it fit the situation, but this practice wastes time and material. The secret is to find out where the bend is needed, mark the conduit accordingly, and make the bend in the right place. This practice saves time and material. Before you can determine where to place your bender on the conduit, there are some things you must know. First, there are two lengths on the conduit that must be considered, from one end of the conduit to the 90° bend and then from the 90° bend to the other end of the conduit. The shorter of these two lengths is called the stub end and the longer is the running end. Second, the radius of the bend takes up a part of the stub. This part of the stub is called take-up and is shown in Figure 3 the amount of take-up depends on the type and size of the conduit you are bending Table -1

Figure: 3 Conduit bending terms

Table-1 Conduit take-up
Amount of Take-Up for 90° Bends Using an EMT Bender
Size and Type of Conduit	Take-Up
1/2-inch EMT	5 inches
3/4-inch EMT or 1/2-inch rigid steel*	6 inches
1-inch EMT or 3/4-inch rigid steel*	8 inches
1 1/4-inch EMT or 1-inch rigid steel*	11 inches

In the following example, you are going to make a 90° bend using 1/2-inch EMT conduit and the EMT bender. You are going to run the conduit from the top of a panel to the ceiling and then horizontally along the ceiling. Measure from the top of the panel to the ceiling. This will give you the stub length of 18 inches. Measure 18 inches from the end of the conduit and make a mark (Figure 4).

Look at Table 1 to find out what the take-up is for 1/2-inch EMT conduit. The take-up is 5 inches. Measure back 5inches from the first mark toward the end of the conduit and make a second mark as shown in Figure - 4

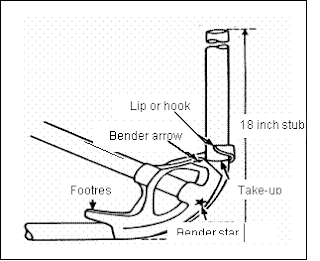
Figure -4 placing the bender to make a 90° bend

Hold the bender in one hand with the lip on the floor pointed toward the stub end. Use the other hand to place the conduit in the bender. Align the bender arrow with the take-up mark. Put one foot on the footrest and hold the handle with both hands. To make the bend, apply pressure on the footrest as you pull on the handle until the handle is parallel with the floor. It is OK to go slightly beyond 90° with the bend, in fact it is preferred, because it is easy to bring it back to 90°.

You should now have a 90° bend with an 18-inch stub Figure 4. To see whether the bend will fit properly, place it next to something that has a right angle (for example, in the corner where the floor and wall meet).

Figure 3-6. 90° bend with an 18-inch stub

If the bend is more than 90°, you can stand on the running end and push out on the stub end, a little at a time, until it is 90°. If the stub is too short or if the conduit is too long to push back, place the handle of the bender over the end of the stub and, with one foot on the conduit on the floor, spring the stub back (right-angle bends should always be made with the conduit and the bender on the floor).

In this example, you are going to make a 90° bend in the conduit and run it along the wall. The first thing you must do is establish a reference point using the following steps:

Step 1: Measure the distance from the outside edge of the knockout to the wall at box a (Figure -5).

Step 2: Transfer that measurement above box A and across from box B. Mark a reference line (Figure -5).

Step 3: Measure the distance from the outside edge of the knockout to the ceiling at box B (Figure -5)

Step 4: Transfer that measurement across from box B and above box A. Mark a reference line. Where the two lines cross is the reference point (Figure -5).

Step-5: Measure from box A to the reference point and add this measurement to the measurement between box B and the reference point. Deduct the gain (Table -1). This will give you the length for the piece of conduit you need to run between boxes A and B (Figure -5).

Figure -5 90° bend

Loss of Head in Bends:

The loss of head, due to bends in a pipe, depends upon three factors. First, loss due to change of direction of the water in the pipe; second, loss from friction as in an ordinary straight length of pipe; third, loss due to enlargements or contractions in the bend, such as are formed when the undreamed ends of pipe are screwed into ordinary elbows.

The second and third losses also apply to couplings and tees, and the loss is about the same as for bends of equal diameters. The loss of head for change of direction differs with the angle and with the radius of the bend. That is, there is less loss for change of direction in a 45 degree bend than in a 90 degree bend, and the loss is greater in a bend of one diameter radius than in one with a radius of two diameters. The loss in a 90 degree bend with a radius of five or more diameters and uniform smooth interior bore is no greater than in an equal length of straight pipe. In other words, there is practically no loss for change of direction in a bend of greater radius than 5 diameters.

The head lost in a 90 degree bend of less than 5 inch diameter and of the radius commonly found in practice (Radius=Diameter) with square undreamed ends of pipe screwed into the fitting, Fig-1 is found by experiment to equal the head lost in a length of pipe of about 100 times the diameter of the fitting.* The loss of head is divided into:

Fig-7

*Thus 100 diameters of 2-inch pipe=200 inches of straight 2-inch pipe.

Loss of head due to change of direction . . . . . .	38 diameters
Loss of head for entry with ordinary undreamed ends. .	58 diameters
Loss of head from friction due to length. . . . . .	4 diameters
Total	100 diameters

In pipes of larger diameter than 5 inches, these values would hold true only for the loss of head due to change of direction, as the pipes are not relatively as thick, nor the enlargements of the elbows relatively as greatThe loss of head when the ends of the pipe screwed into the fitting are reamed, as shown in Fig-2 is found by experiment to be equal to the loss of head in a pipe equal in length to about 50 diameters of the fitting. This loss of head is divided into:

Fig-8

Loss of head due to change in direction 38 diameters

Loss of head due to enlargement of the bend 8 diameters

Loss of head from friction due to length of fitting 4 diameters

Total=50 diameters

The loss of head in a bend of five or more diameter radius, with flush interior joints, Fig-3 is equal to the loss of head in a length of pipe four diameters of the fitting. This is comparatively shown as follows:

Loss of head due to change of direction	0 diameters
Loss of head due to enlargements of the bend	0 diameters
Loss of head from friction due to length of pipe	4 diameters
Total	4

From the foregoing it will be seen that the least possible head is consumed by using fittings of large radius with flush joints. That when common fittings are used the loss can be reduced to one-half by reaming the ends of the pipe with a triangular-shaped reamer, the length of which is just double the base.

Table -2 Values of Coefficient n


r R =	R=r	R=1.12r	R=1.25r	R=1.4r	R=1.6r	R=2r	R=2.5 r	R=3.3r	R=5r
n	1.98	141	.98	.66	.44	.29	.21	.16	.14

Fig-9

The loss of head due to bends can be calculated by the formula:

V₂ h=n 2g

In which h=head lost in feet v = velocity in feet per second g = 32.16 acceleration due to gravity n = a coefficient for the bend.

The value of coefficient n depends upon the ratio between the radius r of the pipe and the radius R of the bend. Table -2 gives values of n corresponding to various values of the ratio r.

Losses in Pipe Bends:

· Bends are provided in pipes to change the direction of flow through it. An additional loss of head, apart from that due to fluid friction, takes place in the course of flow through pipe bend.

· The fluid takes a curved path while flowing through a pipe bend as shown in Fig 1

Fig: 10 Flow through pipe bend

Whenever a fluid flows in a curved path, there must be a force acting radically inwards on the fluid to provide the inward acceleration, known as centripetal acceleration.

This results in an increase in pressure near the outer wall of the bend, starting at some point A (Fig-1) and rising to a maximum at some point B There is also a reduction of pressure near the inner wall giving a minimum pressure at C and a subsequent rise from C to D .Therefore between A and B and between C and D the fluid experiences an adverse pressure gradient (the pressure increases in the direction of flow).

Fluid particles in this region, because of their close proximity to the wall, have low velocities and cannot overcome the adverse pressure gradient and this leads to a separation of flow from the boundary and consequent losses of energy in generating local eddies. Losses also take place due to a secondary flow in the radial plane of the pipe because of a change in pressure in the radial depth of the pipe.

This flow, in conjunction with the main flow, produces a typical spiral motion of the fluid which persists even for a downstream distance of fifty times the pipe diameter from the central plane of the bend. This spiral motion of the fluid increases the local flow velocity and the velocity gradient at the pipe wall, and therefore results in a greater frictional loss of head than that which occurs for the same rate of flow in a straight pipe of the same length and diameter.

The additional loss of head (apart from that due to usual friction) in flow through pipe bends is known as bend loss and is usually expressed as a fraction of the velocity head as, Kv²/2g where V is the average velocity of flow through the pipe. The value of K depends on the total length of the bend and the ratio of radius of curvature of the bend and pipe diameter R/D. The radius of curvature R is usually taken as the radius of curvature of the centre line of the bend. The factor K varies slightly with Reynolds number Re in the typical range of Re encountered in practice, but increases with surface roughness.

Losses in Piping Systems:

Objective: One of the most common problems in fluid mechanics is the estimation of Pressure loss. It is the objective of this experiment to enable pressure loss measurements to be made on several small bore pipe circuit components such as pipe bends valves and sudden changes in area of flow.

Description of Apparatus: The apparatus is shown diagrammatically in Figure 1. There are essentially two separate hydraulic circuit’s one painted dark blue, and the other painted light blue, but having common inlet and outlets. A hydraulic bench is used to circulate and measure water. Each one of the two pipe circuits contains a number of pipe system components. The components in each of the circuits are as follows:

Dark blue circuit:

1. Gate Valve

2. Standard Elbow Bend

3. 90o MITRE Bend

4. Straight Pipe

Light blue circuit:

5. Globe Valve

6. Sudden Expansion

7. Sudden Contraction

8. 150 mm 90o Radius Bend

9. 100 mm 90o Radius Bend

10. 60 mm 90o Radius Bend

In all cases (except the gate and globe valves) the pressure change across each of the component is measured by a pair of pressurized piezometer tubes. In the case of the valves, pressure measurement is made by U-tubes containing mercury.

Theoretical Background: For an incompressible fluid flowing through a pipe (Fig. 2) the following equations apply:

Q = V1A1 = V₂A₂ (continuity) (1)

Z₁ +P₁/ρg +V₁²/2g = Z₂ +P₂/ ρg + V₂²/2g _{hL1 -2} (2)

Head Loss: The head loss in a pipe circuit falls into two categories:

a) That due to viscous resistance extending throughout the total length of the circuit

b) That due to localized affects such as valves, sudden changes in area of flow and bends.

The overall head loss is a combination of both these categories. Because of the mutual interference that exists between neighboring components in a complex circuit, the total head loss may differ from that estimated from the losses due to the individual components considered in isolation.

Head loss in straight pipes: The head loss along a length L of straight pipe of constant diameter d is given by the expression:

h_L + 2f LV²/gd

or f =h_Lgd/2LV²

Where f is a dimensionless constant (i.e. friction factor) which is a function of the Reynolds’s number of the flow and the roughness of the internal surface of the pipe.

Head loss Due to Sudden Changes in Area of Flow:

i) Sudden Expansion - The head loss at a sudden expansion is given by

h_L = (V1-V2)²/2g (4)

ii) Sudden contraction - The head loss at a sudden contraction is given by

h_L = KV₂²/2g (5)

Where K is a dimensionless coefficient which depends upon the area ratio as shown in Table I.

Table 1: Loss Coefficient for Sudden Contractions

A₂/A₁	0	0.1	0.2	0.3	0.4	0.6	0.8	1.10
K	0.50	0.46	0.41	0.36	0.30	0.18	0.06	0

Head loss Due to Bends: The head loss due to a bend is given by the expression:

h_B = K_BV²/2g (6)

Where KB is a dimensionless coefficient which depends on the bend radius/pipe radius ratio and the angle of the bend. It should also be noted that the loss given by this expression is not the total loss caused by the bend but the excess loss above that which would be caused by a straight pipe equal in length to the length of the pipe axis.

Head loss Due to Valves: The head loss due to a valve is given by the expression:

h_L = KV²/2g (7)

Table 2: Loss Coefficient

Valve type	K
Globe valve, fully open	10.0
Gate valve, fully open	0.2
Gate valve, half open	5.6

Experimental Procedure:

1. Open fully the water control on the hydraulic bench.

2. With the globe valve closed, open the gate valve fully to obtain maximum flow through the dark blue circuit. Record the readings on he piezometer tubes and the U-tube. Measure the flow rate by timing the level rise in the volumetric tank.

3. Repeat the above procedure for a total of ten different flow rates obtained by closing the gate valve, equally spaced over the full flow range.

4. With a simple mercury in glass thermometer record the water temperature in the sump tank.

5. Close the gate valve, open the globe valve and repeat the experimental procedure for the light blue circuit.

Report (Data Analysis): In addition to tables showing all experimental results, the report must include the followings:

Dark blue circuit experiment:

a) Obtain the relationship between the straight pipe head loss and the volume flow rate (h_L & Qⁿ) by plotting log h_L against log Q (log h_L vs. log Q).

b) Plot friction factor data versus Reynolds’s number for the straight pipe (L = 0.914 m, D = 13.7 mm). Also, obtain relationship between f & Reⁿ by plotting log f against log Re. Comment on your result by comparing with the literature given equations (i.e. f =0.04 Re-0.16 for 4000<Re<10⁷& f = 0.079 Re-1/4 for 4000< Re < 10⁵ ).

c) Obtain the value of K for the gate valve when it is fully opened and compare with literature (Table 2).

d) Discuss head losses in 90° Mitre and Standard Elbow bend.

Light blue circuit experiment:

a) If head rise across a sudden expansion (13.7 mm / 26.4 mm) is given by expression

h_L = 1.303V₁²/2g

Compare this head rise with the measured head rise. Plot the measured and the calculated head rise.

b) If head loss due to sudden contraction (26.4 mm / 13.7 mm) is given by the expression

h_L = 1.303V₂²/2g

Compare this fall in the head with the measured head loss. Plot the measured and calculated fall in head due to sudden contraction.

c) Obtain the value of K for the globe valve when it is fully opened and compare with literature (Table 2)

d) What is the effect of bend radius on head losses?

Notation:

Q volumetric flow rate, (m3/s)

V mean velocity, (m/s)

A cross-sectional area, (m2)

Z height above datum, (m)

P static pressure, (N/m2)

h_L head loss, (m)

ρ density, (kg/m3)

g acceleration due to gravity, (9.81 m/s2)

f Friction factor

d Diameter of pipe, (m)

L Length of pipe, (m)

K Loss Coefficient

KB Loss coefficient due to bends

Re Reynolds Number

Secondary losses in bends and fittings:

Objectives: It is required demonstrate the secondary losses through different types of bends and fittings.

Experimental Procedure:

1. Close the regulation valve and start the centrifugal pump.

2. Open the valve partially.

3. Wait for steady flow (piezometers readings=constant).

4. Read the differential readings of the peizometers connected to the mite the elbow, the short the enlargement and the contraction.

5. Read the initial volume in the collection tank V1.

6. Observe the time (t) to increase the collected volume to V2.

7. Increase the valve opening.

8. Repeat the experiment tow times.

9. After recording all the required readings, close the valve gradually then stop the centrifugal pump.

Conclusion: We learn here about different types of bends losses and how we will measure it.

Technology & Current World

Monday 18 June 2012

Different Losses in Bend

Loss of Head in Bends:

· Bends are provided in pipes to change the direction of flow through it. An additional loss of head, apart from that due to fluid friction, takes place in the course of flow through pipe bend.

· The fluid takes a curved path while flowing through a pipe bend as shown in Fig 1

Fig: 10 Flow through pipe bend

Whenever a fluid flows in a curved path, there must be a force acting radically inwards on the fluid to provide the inward acceleration, known as centripetal acceleration.

No comments:

Post a Comment